Area Determination of Property Images

April 06, 2013

In a class I am taking, we were given the following problem:

Calculate (rougly) the area of land shaded green, and the area of property in the green land (the grey buildings).

Here is a typical image:

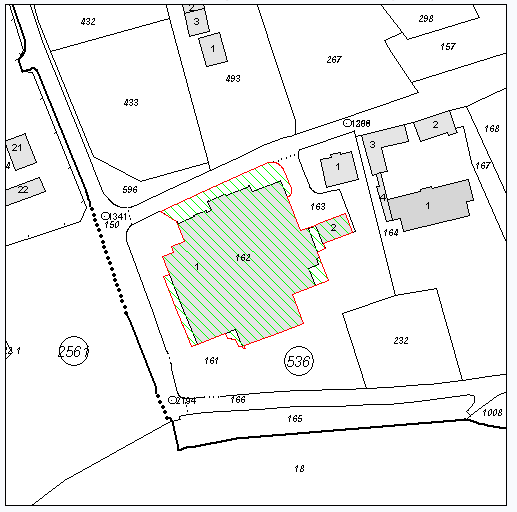
'Sample Image'

My Attempt

Thankfully, reading .PNG files into R is easy

library(png)
library(geometry)

files <- dir("rawimages", full.names=TRUE)
j <- 2
x <- readPNG(files[j])
dim(x)

## [1] 512 517   3

x[1:5,1,]

##        [,1]   [,2]   [,3]
## [1,] 0.9725 0.9804 0.9922
## [2,] 0.9725 0.9804 0.9922
## [3,] 0.9725 0.9804 0.9922
## [4,] 0.9725 0.9804 0.9922
## [5,] 0.9725 0.9804 0.9922

The output of the readPNG() is a three dimensional array (x-coordinate, y-coordinate, RGB values), which is fairly unwieldy. Thankfully, it is easy to coerce matrices in R.

nrows <- dim(x)[1]
ncols <- dim(x)[2]
total <- nrows * ncols

dim(x) <- c(total, 3)

Note! R stores it's matrices as vectors, by column.

If you’ve played around with matrices, you’ll have noticed that for a 2-dimensional matrix, x[3] will return the element x[3,1]. Thus, the first 5 elements of the new coerced x is equivalent to the above x[1:5,1,] command (the first 5 elements in column 1).

head(x)

##        [,1]   [,2]   [,3]
## [1,] 0.9725 0.9804 0.9922
## [2,] 0.9725 0.9804 0.9922
## [3,] 0.9725 0.9804 0.9922
## [4,] 0.9725 0.9804 0.9922
## [5,] 0.9725 0.9804 0.9922
## [6,] 0.9725 0.9804 0.9922

To make sure plotting gives the same orientation, we need to flip things around, since graphs start the origin at the bottom left, while the data structure of the PNG will be starting from the top left.

yvals <- rep(nrows:1, ncols)
xvals <- rep(1:ncols, each=nrows)

head(cbind(xvals, yvals))

##      xvals yvals
## [1,]     1   512
## [2,]     1   511
## [3,]     1   510
## [4,]     1   509
## [5,]     1   508
## [6,]     1   507

Now, we are ready to do some analysis. At first glance, we want to be able to retrieve the red line (or the green area), and the grey area inside that region. It seemed natural to start with k-means clustering, to get a better picture of the different color groups.

km.0 <- kmeans(x, 5, 10)
km.0$centers

##     [,1]   [,2]   [,3]
## 1 0.8980 0.8980 0.8981
## 2 0.0000 0.1789 0.0000
## 3 0.9985 0.9989 0.9996
## 4 1.0000 0.0000 0.0000
## 5 0.8392 0.8392 0.8392

these <- km.0$cluster==4

Recall that the second column is the green channel (so we would expect the green points to have negligable values in the 1st and 3rd, but high in the second). However, the k-means clustering doesn’t seem to pick them up (weird). We were able to pick up the red and the grey though (red shown below).

plot(xvals, yvals,
    col=apply(x, 1, function(a) rgb(a[1], a[2], a[3])),
    pch=18, cex=0.2)
points(xvals[these], yvals[these], cex=1)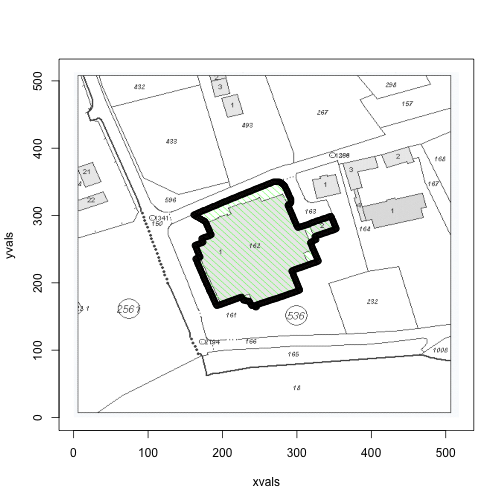

plot of chunk unnamed-chunk-6

Unfortunately, there are images that have multiple areas denoted by a red border. Since we only care about those shaded green, it is not enough to use the red points. We overstep this problem by restricting our attention to the neighbours of the green area. To get the green values, we shall hazard an educated guess as to the form of the RGB.

green <- x[,2] > 0.9 &
         x[,1] < 0.1 &
         x[,3] < 0.1

Let’s check to see if we’re right

plot(xvals, yvals,
    col=apply(x, 1, function(a) rgb(a[1], a[2], a[3])),
    pch=18, cex=0.2)
points(xvals[green], yvals[green], cex=1)

plot of chunk unnamed-chunk-8

Nice. Okay, so now we can create a rectangle around this area (with some slack, to ensure the red border lies inside the area) that we are interested in.

slack <- 5
xmin <- min(xvals[green])-slack
xmax <- max(xvals[green])+slack
ymin <- min(yvals[green])-slack
ymax <- max(yvals[green])+slack

x[xvals <= xmin | xvals >= xmax | yvals <= ymin | yvals >= ymax,] <- c(1,1,1)

The restricted diagram looks like so:

plot(xvals, yvals,
    col=apply(x, 1, function(a) rgb(a[1], a[2], a[3])),
    pch=18, cex=0.2)

plot of chunk unnamed-chunk-10

Great! Now we can ignore the green points, and focus our attention on the greys and reds. In the above diagram, we come across another potential problem: there are grey areas in the image that aren’t inside the red boundary. Our algorithm handles that nicely though.

grey <- x[,1] >0.80 & x[,1] < 0.95 &
        x[,2] >0.80 & x[,2] < 0.95 &
        x[,3] >0.80 & x[,3] < 0.95
greys <- which(grey)

red <- x[,1] > 0.95 &
       x[,2] < 0.05 &
       x[,3] < 0.05
reds <- which(red)

The Algorithm

The crux of the algorith is the use of the areapl() function in the splancs library. This function takes a sequence of points that join up to make a polygon, and calculates the area. Importantly, the points must be sequential around the polygon. Hence, the variable red is insufficient. The algorithm is as follows: for each row,

retrieve the first and last red point
retrieve the first and last grey point within the red points

min.red <- c()
max.red <- c()
min.grey <- c()
max.grey <- c()
groups <- split(1:total, yvals)
for(i in 1:nrows) {
  row <- groups[[i]]
  row.reds <- row[row %in% reds]
  if (length(row.reds) < 2) next
  min.red <- c(min.red, row.reds[1])
  max.red <- c(max.red, row.reds[length(row.reds)])
  row.greys <- row[row %in% greys]
  # greys must be within the range of red
  row.greys <- row.greys[row.greys > row.reds[1] & row.greys < row.reds[length(row.reds)]]
  if (length(row.greys) < 2) next
  min.grey <- c(min.grey, row.greys[1])
  max.grey <- c(max.grey, row.greys[length(row.greys)])
}

red.pts <- cbind(c(xvals[min.red], rev(xvals[max.red])),
                 c(yvals[min.red], rev(yvals[max.red])))
grey.pts <- cbind(c(xvals[min.grey], rev(xvals[max.grey])),
                  c(yvals[min.grey], rev(yvals[max.grey])))

The polygons we retrieve are shown below.

plot(red.pts, col=1, type='b')
points(grey.pts, col=2, type='b')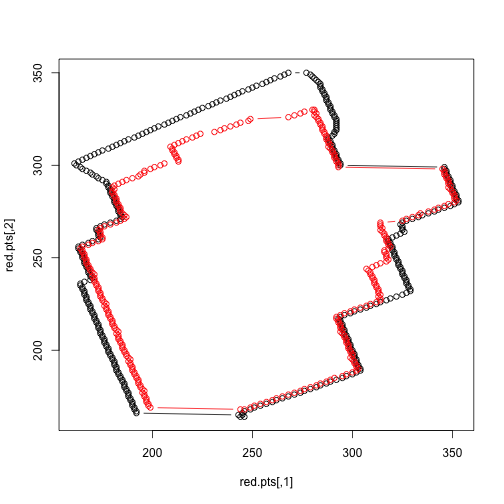

plot of chunk unnamed-chunk-13

We can now calculate a rough area.

library(splancs)
c(areapl(red.pts), areapl(grey.pts))

## [1] 22306 18594

We can now create a function with takes a .PNG file path (and a jump parameter, which determines the number of rows to skip), and returns a plot of the original, the polygons, and the area of the polygons:

area <- function(file, jump=1){
  x <- readPNG(file)

  nrows <- dim(x)[1]
  ncols <- dim(x)[2]
  total <- nrows * ncols

  yvals <- rep(nrows:1, ncols)
  xvals <- rep(1:ncols, each=nrows)
  dim(x) <- c(total, 3)

  plot(xvals, yvals,
       col=apply(x, 1, function(a) rgb(a[1], a[2], a[3])),
       pch=18, cex=0.2)

  green <- x[,2] > 0.9 &
           x[,1] < 0.1 &
           x[,3] < 0.1

  slack <- 5
  xmin <- min(xvals[green])-slack
  xmax <- max(xvals[green])+slack
  ymin <- min(yvals[green])-slack
  ymax <- max(yvals[green])+slack

  x[xvals <= xmin | xvals >= xmax | yvals <= ymin | yvals >= ymax,] <- c(1,1,1)

  grey <- x[,1] >0.80 & x[,1] < 0.95 &
          x[,2] >0.80 & x[,2] < 0.95 &
          x[,3] >0.80 & x[,3] < 0.95
  greys <- which(grey)

  red <- x[,1] > 0.95 &
         x[,2] < 0.05 &
         x[,3] < 0.05
  reds <- which(red)

  min.red <- c()
  max.red <- c()
  min.grey <- c()
  max.grey <- c()
  groups <- split(1:total, yvals)
  n <- floor(nrows/jump)
  for (i in 1:n) {
    row <- groups[[i*jump]]
    row.reds <- row[row %in% reds]
    if (length(row.reds) < 2) next
    min.red <- c(min.red, row.reds[1])
    max.red <- c(max.red, row.reds[length(row.reds)])
    row.greys <- row[row %in% greys]
    # greys must be within the range of red
    row.greys <- row.greys[row.greys > row.reds[1] & row.greys < row.reds[length(row.reds)]]
    if (length(row.greys) < 2) next
    min.grey <- c(min.grey, row.greys[1])
    max.grey <- c(max.grey, row.greys[length(row.greys)])
  }

  red.pts <- cbind(c(xvals[min.red], rev(xvals[max.red])),
                   c(yvals[min.red], rev(yvals[max.red])))
  grey.pts <- cbind(c(xvals[min.grey], rev(xvals[max.grey])),
                    c(yvals[min.grey], rev(yvals[max.grey])))

  points(red.pts, col=2, type='b', cex=0.5)
  points(grey.pts, col=1, type='b', cex=0.5)
  return(c(areapl(red.pts), areapl(grey.pts)))
}

files <- dir("rawimages", full.names=TRUE)
for (i in c(1,3,4)) {
  print(area(files[i]))
}

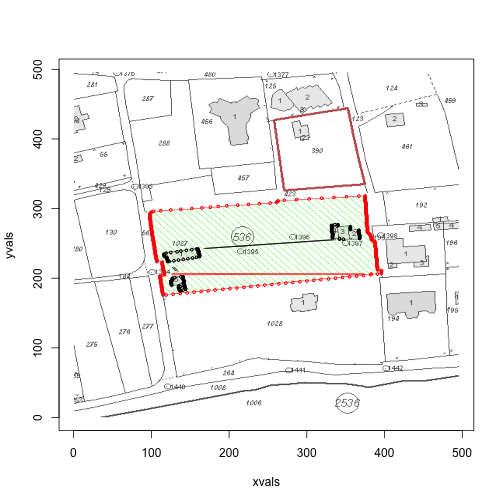
plot of chunk unnamed-chunk-16

## [1] 32394  1438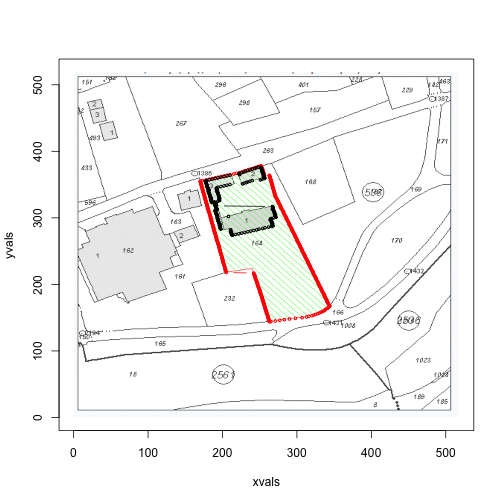

plot of chunk unnamed-chunk-16

## [1] 20930  4111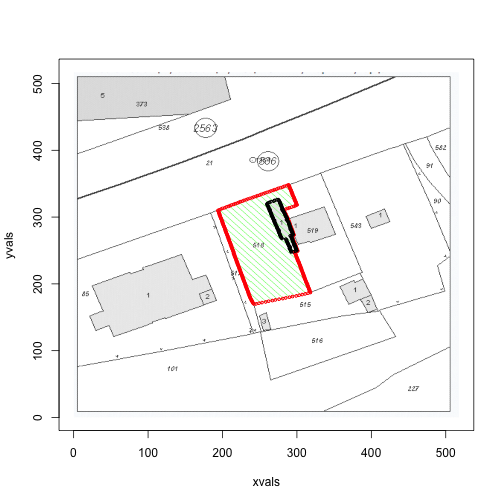

plot of chunk unnamed-chunk-16

## [1] 13334  1140

A Little Extra

If you take a look at the first image, in the above loop, we see that there is anomaly in the red border. Upon further inspection, it turns out that there are times when there will be no red points on the left border, but two red points on the right border (the algorithm ignores situations when there is only one red in a row).

One possible solution is to increase the jump:

area(files[1], jump=5)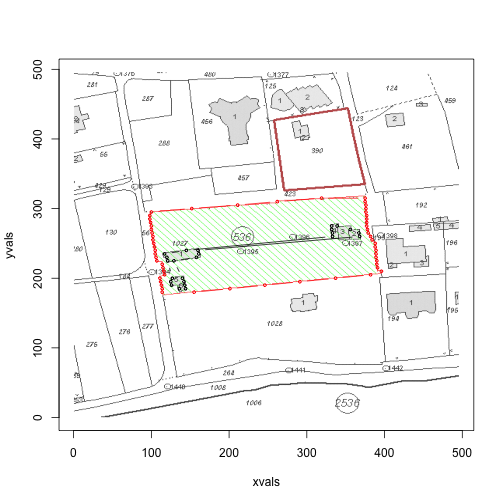

plot of chunk unnamed-chunk-17

## [1] 32412  1848

Alternatively, we can iterate through the min.red and max.red values, and see if there are any anomalies. But this is equivalent to putting more significant figures on an already crude estimate - we’ll leave it here for today.

r
statistics

Jekyll and Knitr

April 05, 2013

With Knitr, anything is possible (and ridiculously simple). Creating reproducible R code in your jekyll blog is as simple as

library(knitr)
render_jekyll(highlight="pygments")
knit('file.Rmd')

In your .Rmd file, instead of displaying code (using the liquid templates + pygments)

{% highlight r %}
library(knitr)
{% endhighlight %}

we now have

```{r}
library(knitr)
```

That’s it, basically. You will probably want to set up some options (such as defining a path for images). I have created a .R file to automate everything for this blog, which you can find here.

Helpful resources:

jfisher’s blog post
Yi Hui’s website

r
statistics

Pitch Perfect

December 24, 2012

Pitch Perfect

Here is an Acappella mashup of Just The Way You Are (Bruno Mars) and Just a Dream (Nelly), from the soundtrack of the movie Pitch Perfect.

Such a beautiful arrangement.

music

Christmas Party

December 23, 2012

Christmas@Yale. Joyful times.

photography

Fun Algorithms Problem

December 06, 2012

A while back, I bought the venerable book, Introduction to Algorithms. One of the first problems that I did and remembered was the following:

Describe a $\Theta(n \log n)$ time algorithm that, given a set $S$ of $n$ integers and another integer $x$, determine whether or not there exist two elements in $S$ whose sum is exactly $x$.

(A) Solution

The trick I employed was to consider the set $S - x/2$, remove duplicates, and then take absolute values. If you think about it, the condition that two elements in $S$ sum to $x$ is equivalent to checking for duplicates in the new set. So, we’ve reduced the problem to a simpler one - finding duplicates - which we know is of order $\Theta(n \log n)$ (it can’t be slower than sorting, which by quicksort is of order $\Theta(n \log n)$).

In python, it’s easy to determine the presence of duplicates by simply making use of the set function. Alternatively, you can write a quicksort like algorithm, as demonstrated below.

def has_sum(l,y):
    mid = float(y)/2 # mid value of y
    if len([x for x in l if x == mid]) > 1:
        return True # if two mid values, return true
    l2 = set([x-mid for x in l]) # remove duplicates
    l3 = [abs(x) for x in l2] # get absolute
    if True:
        # option 1: check for difference in size if we remove duplicates
        l4 = set(l3)
        return len(l3) != len(l4)
    else:
        # option 2: do a quick sort
        return qsort(l3)

def qsort(l):
    if len(l) == 1 or len(l) == 0:
        return False
    if len(l) == 2 and l[0] == l[1]:
        return True
    piv = l[0]
    l1 = []
    l2 = []
    for x in l[1:]:
        if x == piv:
            return True
        elif x > piv:
            l1.append(x)
        elif x < piv:
            l2.append(x)
    return qsort(l1) or qsort(l2)

if __name__ == "__main__":
    l = [6,7,45,2,100,42,9,17,18,13,22,25,33]
    print has_sum(l,29)

← Older